この世の中にはたくさんの数字で溢れています。特定の基準を決め、そのルールに従って集めてもその数は数え切れません。

もし、2つのグループがあり、パッと見、違いがあるようです
みなさんなら、どうしますか?

平均をとって数字で比べてみればいいのでは?

そうですね
平均は小学生5年生で習います
私は、小学生4年生から6年生まで研究を指導したことがあります。そうしますと、「平均」という言葉を使いますと、反応する子と反応しない子に分かれることに気づきました。
尋ねたところ、小学校4年生の子が

習ってない!
と元気よく答えてくれました。

決まった条件で実験すると特定の数字に結果が集まりました
以前のブログで、繰り返し実験のお話をしました。
子どもたちが不満を言っていましたね(笑)。そのときのお話です。
実験を繰り返し、子どもたちが黒板に結果の「数」を書いていきます。どんどん書いていきますと、15(仮)に近づいていきました。

先生、これって15に近づいているんじゃないの?

よく気づいたね
これってどういう意味なんだろう?
子どもたちにグラフ用紙を与えて、すべての実験結果をプロットしてもらいました。

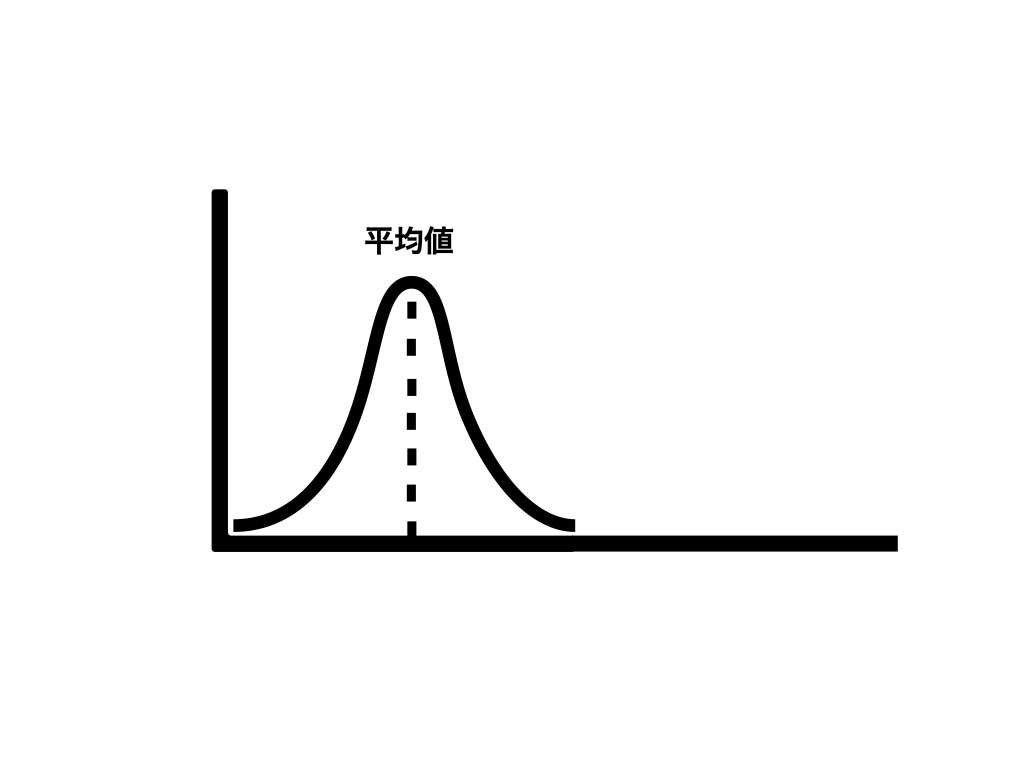
先生、中心が高くて左右対称の山になっているよ!
子どもたちは「言葉」は知りませんが、子どもたちの結果が「正規分布」していることに気が付きました。

正規分布の中心が平均の値になります

じゃ、平均を計算してみましょう
小学校5年生の子、平均てどうやって計算する?

先生、今って理科みたいな実験じゃないの
何で算数をするの?

そうだね

学校では覚えることが多い理科だけれども、君たちは誰も結果を知らないことを今研究しています

つまり世界初
世界初になる人は再現性(繰り返し実験をやって同じ結果になること。)を見せなければならないんだよ

そのためには「数字」で語らなければならない
その手段が平均ってわけ

ふ~ん
こんなやりとりのあと、指名されたお子さんは黒板に平均を求める式を書いてくれました。
平均=(◯+□+◇+△+☆)÷5(今回の場合)

そうだね
実際にはもっと数が多いから電卓で計算していいよ
そうしますと、子どもたちの1人が気が付きました。

先生、さっき描いた実験結果の山の中心と平均の値が同じになったよ!
そうなんです。平均は、算数ではただの計算結果ですが、科学ではたくさんの実験結果を説明するための値になるんです。

へ~
計算となると嫌なのに、なんか変な感じ
小学校5年生で習う平均は計算方法です。基礎ですね。
そして、科学の世界では、平均の値は実験結果をまとめる代表となる数字となります。小学5年生で習った平均は、中学生、高校生、大学生、大学院生、研究者になっても、実は、ずっと使います。
科学雑誌で出版される論文では、平均値はいたるところで見られます。

算数と理科が自然に融合すれば、本当の科学は子どもたちにもっと身近になりますね



コメント